勾股定理较早出现在古代数学的《九章算术》里面，而我们学生较早开始学的时候是在小学的时期。小学数学中已经有了对勾股定理的介绍，同学们也是会简单的使用。勾股定理可以说是一个数学定理，在古代有很多跟勾股定理相关的问题，我给出了下面的两个，一个是池中之葭，一个是折竹问题，我们来看这个问题是什么样的。

　　《九章算术》是我国古代的数学著作，就像古希腊《几何原本》一样，一直作为算学教科书。《九章算术》是以数学问题集的形式编写，共收集了200多个问题。按性质分类，每类问题为一章，有方田，粟米、衰分，少广、商功，均输、赢不足、方程，勾股九章，故称九章算术。在勾股章中有好多有意思的问题。

　　一、池中之葭(芦苇)

　　今有池方一丈，葭生其中央，出水一尺。引葭赴岸，适与岸齐。问水深、葭长各几何?

　　题目的意思已经说得很明白了，我就不再另行翻译了。通过的方程很容易解答。

　　这是现在的解法，我们发现，这道题还是比较容易的。然而在古代数学发展的早期，数学理论还不是很完善，计算工具和方法还十分原始，对于古人来说，要解决这样一个题目并不是很容易。古人使用的是图示法。

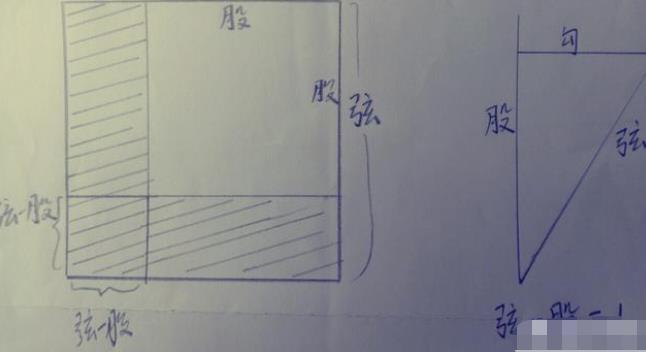
　　图的右半部分可以说是题意的图示，水深为股(未知)，葭长为弦未知，池方的一半(5尺)为勾，还有一个已知的就是弦股差1尺(葭生其中央，出水一尺)。

　　在直角三角形中是满足勾股定理的，也是就弦方减去股方等于勾方。根据这个关系可以画出左边的图。

　　整个正方形表示弦方

　　白色正方形为股方

　　阴影部分的面积即为勾方，这部分是已知的为25.在阴影部分的左下角是一个面积为1的正方形。将这个小正方形的面积减去，两个长方形的面积为24，就比较容易知道长方形的长(股)为12。于是水深12尺，葭长13尺。其实这个方法也就是方程解法的几何意义。

　　二、折竹问题。

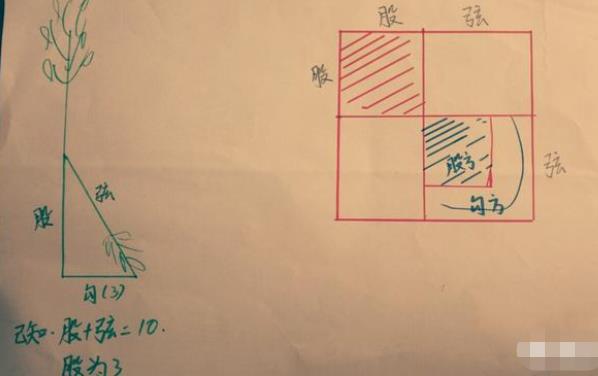
　　今有竹高一丈，末折抵地，去本三尺，问折者高几何?《九章算术》勾股章第十三题。

　　还是翻译一下吧，意思是有一根一丈高的竹子，竹梢被风吹折，恰好接触地面，距离竹根三尺，问竹子折断的地方距地面多高?

　　以股加弦为边长作一个大正方形，其中红色及蓝色阴影部分，均表示股方，右下角的白色折尺形区域表示勾方。请读者自行思考。

　　这是古代中增强勾股定理的两个问题，在现代也是有很多跟勾股定理相关的问题，你们是怎么解决的呢?建议同学们自己下来多搜集一些类似的题目，研究一下如何解答。