函数是贯穿小学到大学一个重要的知识点，函数有三大要素，基本上学到搞中国的时候就知道了。分别是定义域，值域跟对应法则，而定义域跟和值域就组成了数的集合。集合在函数里需要的一个要素，下面我就来解释一下集合和函数的关系，在高一数学的学习的时候，我们先学习的是集合的概念，然后学了映射的概念，较后学了函数的概念。这样的安排其实是有很大的联系的，能够让学生更好的理解函数的定义。

　　1、谈谈集合

　　集合是指具有某种特定性质的事物的总体，集合具有性，确定性和无序性。比如一个班的学生可以看作一个集合，26个英文字母可以看作一个集合，就算三个同学在一起也可以看作一个集合，的有理数也可以看作一个集合，称为有理数集。

　　2、谈谈映射

　　设A、B是两个非空集合，如果存在一个法则f，使得对A中的每个元素a，按法则f，在B中有确定的元素b与之对应，则称f为从A到B的映射，记作f：A→B。

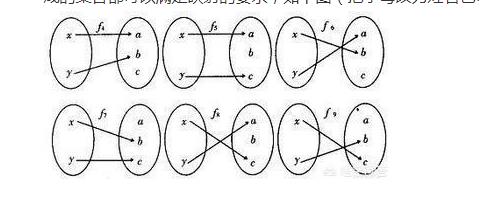
　　可以知道映射对两个集合的要求仅为非空集合，所以不管是一个班的集合还是26个英文字母组成的集合都可以满足映射的要求，如下图(把字母改为姓名也可以)。

　　3、谈谈函数

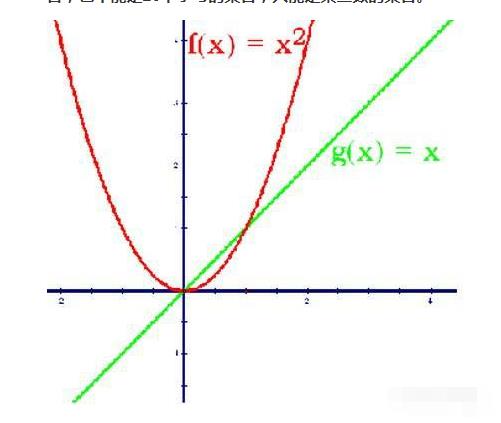
　　函数是从非空数集到非空数集的映射，可见函数其实也是一种特殊的映射，而且要求是一一映射或者多对一的映射。函数对集合的要求不仅是非空集合，还得是数集，不能是一个班的集合，也不能是26个字母的集合，只能是某些数的集合。

　　综上所述，函数是两个数集间的映射，离开集合便无法讨论函数。如果同学们还有什么疑问，请可以关注小编，谈谈你对函数和集合的看法。