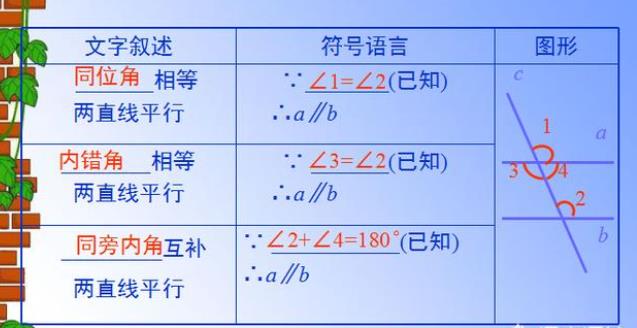
涉及同位角,内错角,同旁内角的题目该怎么解?同位角,内错角,同旁内角三个角是学生经常容易搞混的,其实光是从概念上就可以看得出来的。几何题目中考同位角,内错角,同旁内角的题还是相当多的,想正确解答,我想还是应该掌握这类题目的一个基本的解题思路,下面我给出遇到同位角,内错角,同旁内角问题的常用的解答思路,并给出例子。
同位角,内错角,同旁内角,这三类角是在相交线与平行线这章才被引入的新概念。
平面内两条直线的位置关系有相交和平行两种(重合也就平行了。)
如果两条直线相交的话,必然会出现邻补角和对顶角。
领补角相加等于180度,对顶角是相等的。
两直线垂直是特殊的相交,会产生直角。
例题一、试判断下图中任意两条直线的位置关系,
并找出哪些是“领补角”、哪些是“对顶角”和哪些是“直角”。
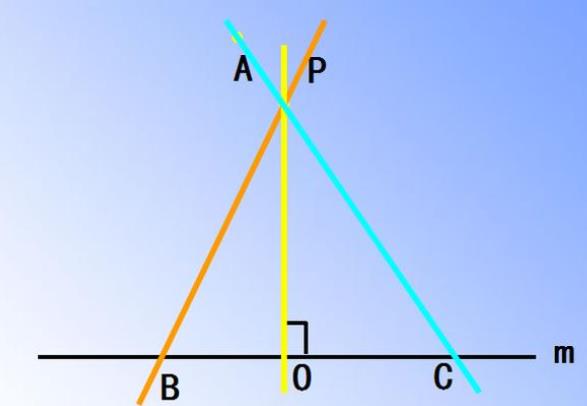
通过例题一的学习,我们知道任意两条直线都不平行,如果两条直线平行的话用什么样的条件去判断呢?
这就引入了三类角:“同位角,内错角,同旁内角”,这三类角就是判断平面内两条直线是否平行的条件。
例题二、
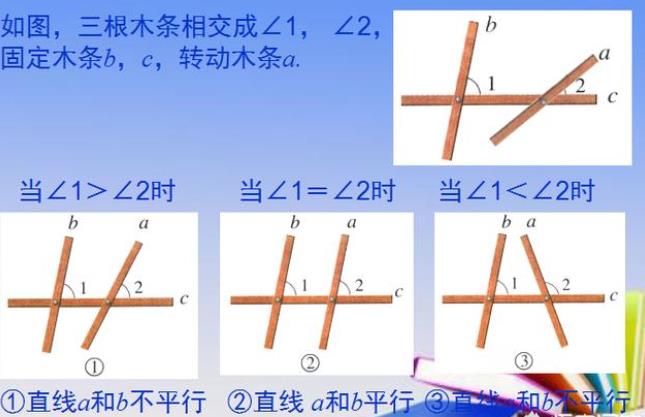
1、同位角的概念:
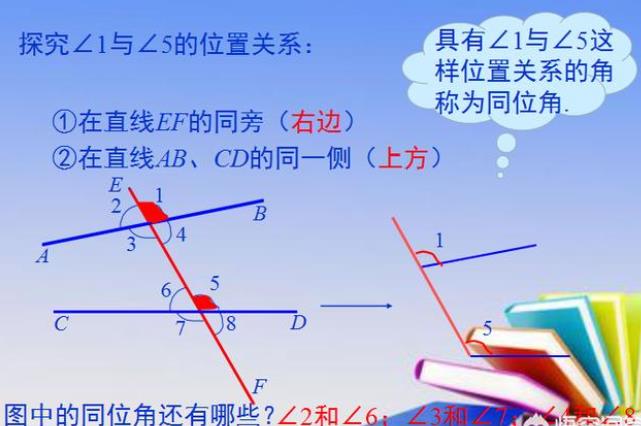
如何在具体图形中找到同位角
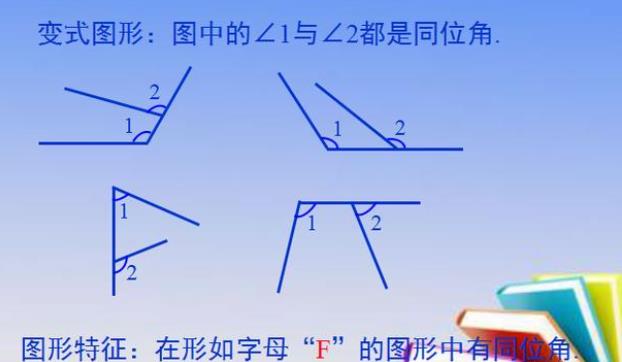
总结归纳

2、内错角的概念:
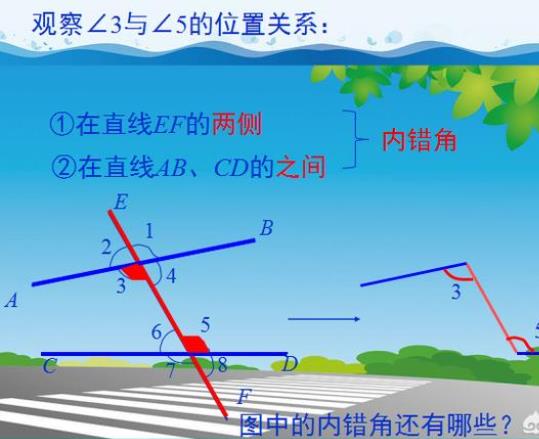
如何在具体图形中找到内错角
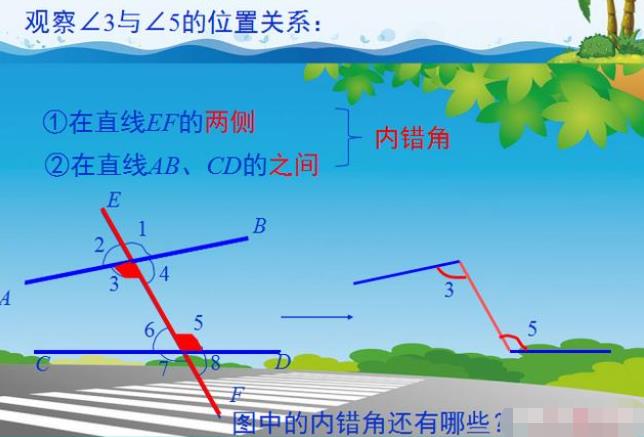
3、同旁内角的概念:
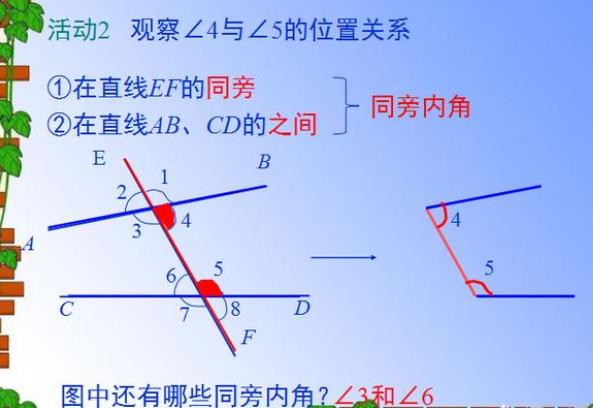
如何在具体图形中找到同旁内角

总结归纳
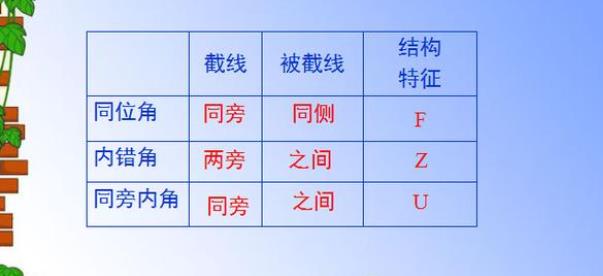
较后总结归纳判定两条直线平行的方法: