时针与分针12点重合后，再转到12点，能重合几次?这个问题是一道小学低年级钟表时针和分针的问题，其实也可以理解为路程中相遇和追及的问题。小学二年级和小学六年级的学生在处理这类问题时，通常用到的方法是不一样的。我给你们分享三种解答时针与分针12点重合后，再转到12点，能重合几次?问题的方法，同学们参考一下：

　　回答一：重合11次。低年级学生可直观推测得到这一结果，高年级学生可用算术方法计算为：

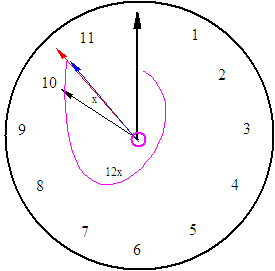
　　12÷〔60÷(60-5)〕=11(次)。但用方程来解学生比较容易理解：设时针和分针从上次重合到下次重合所需时间为x小时，则在这x小时中，时针走了5x格，分针走了60x格，分针与时针再次重合时，分针需要比时针多走一圈即60格，可得方程为60x-5x=60，解得x=12/11(小时)。于是，12小时内重合的次数为12÷(12/11)=11(次)。

　　回答二：这是一道关于“钟表中的数学问题”，需要说明的是：这不是二年级的数学题。分析如下：

　　第一，钟面的一周分为60个小格，每5个小格为一大格，当分针走一周60个小格时，时针正好走5个小格，所以时针的速度是分针的1╱12，也就是分针走一个小格，时针走1╱12小格。

　　第二，有一种数学思维叫类比，比如可把等差数列类比为植树问题，那时针钟问题我们可类比为行程问题，即相遇或追及。

　　第三，因时针比分针慢，本题可看做钟面上的追及问题，分针时针12点重合，可理解为它们的路程已相差60格，这就是追及路程，也是圆周上追及问题的隐含条件(追及路程是一个圆周长)。

　　第四，本题是类比为追及问题，追及时间=追及路程/速度差，追及路程是60格，速度差是1-1╱12，因此，分针每走60╱(1-1╱12)=61又1╱11(分)与时针相遇一次!

　　因此，12小时相遇11次!

　　回答三：答：重合11次。从12点重合出发(不计次)，1点多不到2点重合一次，2点多不到3点重合一次，……重合时不断接近下一个钟点，一直到11点多再重合那一次，就是12点整再次重合。