难题的难度在于它隐藏了直接的解题思路,即通过应用特定的公式或定理直接求解。换句话说,要使用某个公式或定理,我们必须通过“搭桥”,也就是用数学术语来说就是“转化与化归”,来满足使用该公式或定理的条件。然而很大程度上,甚至我们都不清楚应该使用哪个知识点来突破难题。

一、排列组合难题怎么解决?
在这种情况下,我们需要回归到问题的本质,从问题的根源寻找突破口。举例来说,让我们考虑今天要讲的概率统计问题。其本质其实是排列组合,只是后来根据一些明显的特征将其归类为不同的情况。只是符合某些特点的情况才能够使用特定的模型。因此,从问题的本源出发,这也是近几年高考对数学思维考察的一个明显趋势。
以下是排列:
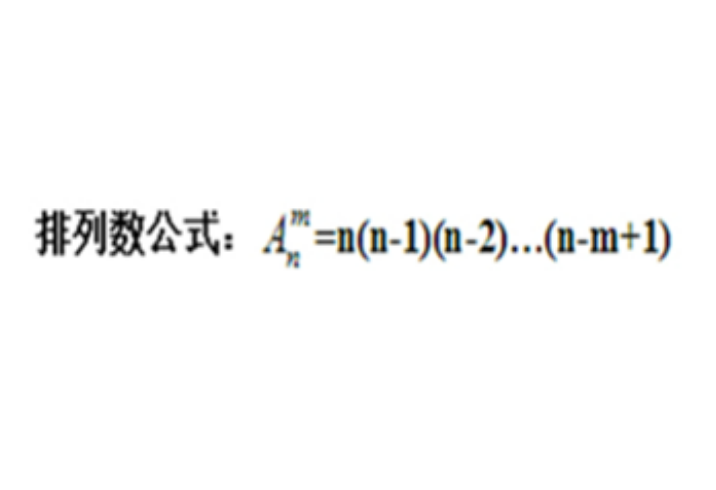
公式解释:排列公式就是从n个不同元素中,任取m个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
我们将公式进一步转化一下:
A(m,n)= n(n−1)(n−2)⋯(n−m+1)=n!/(n−m)!
注意:①排列的有序性,这是与组合的一个及其重要区别。
②m,n为自然数。A(0,n)代表的是不选,只有一种情况即为1。
③上式中n-m+1可以联想类比数列的通项。
以下是组合:
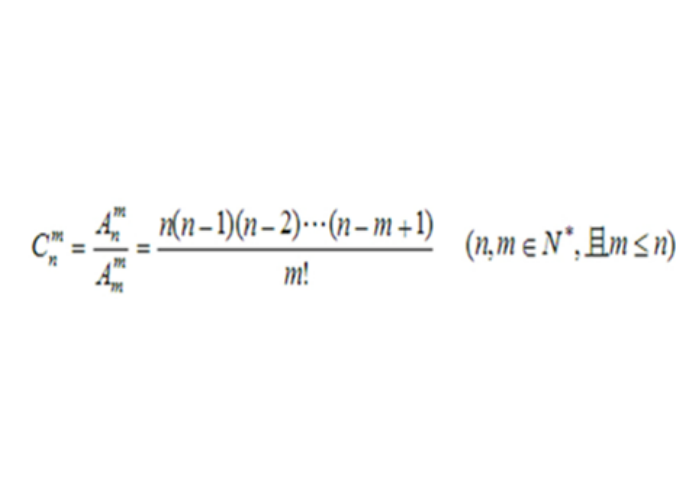
注意:组合的无序性(指的是组内元素没有先后顺序)
以上两个公式说明的是一个“个数”的概念。这与概率有什么关系呢?概率公式P(A)=m/n,其中P(A)表示事件A发生的概率,“m”表示事件A发生的总数,“n”表示总事件发生的总数。
那么,这里的m、n对应着A(m,n)或C(m,n)。所以,概率统计题目内在基础就是排列组合。排列组合没有搞清楚,概率统计一定学不明白。
我们看一个最近很火的,与现实生活息息相关的中奖问题。有三种颜色的球27个,每种颜色个数为9个,放在一个不透明的箱子里,随机摸出9个球,问三种颜色的球配比概率最高的组合是?
【解析】只有3种颜色的球,即可将每种颜色看做是一个组【分类】。组合方式的集合为【(0,0,9)、(0,1,8)、(0,2,7)、(0,3,6)、(0,4,5)、(1,1,7)、(1,2,6)、(1,3,5)、(1,4,4)、(2,2,5)、(2,3,4)、(3,3,3)】共12种,其中数字代表不同颜色球的个数,每个小组的个数之和一定是9(取9个球)。(组合问题,无序性)
这个题再引申一下,若求刚好把其中三种颜色的球全拿出来,概率是多少?
总结一下:本题的解题题眼关键之处在于三种颜色的分组。若在高考时,一时不能准确判断,遇到此类题,穷举也不失一种很好的方法。
有了以上基础,让我们一起来总结一下高考概率问题的求解方式。
二、高考概率综合大题的解题思路总结
常规概率问题:即高中课本上很多关于概率统计的知识点模型(古典概率、几何概型、超几何、二项分布、条件概率、全概率、贝叶斯;努伯力实验、泊松分布、线性回归…等等)。那些类型的参数适合与导数或数列可以组合?
遇到这类题,首先理清要求的发生事件和总事件,其次找出该事件发生符合上述的那种模型,进而计算出事件的发生次数,求出相关概率或概率密度。
难点:然而要正确的解答确不是很容易的,在事件次数分类计算时,很容易出现遗漏的情况或者说事件分类本身就十分困难。其次解题使用的模型张冠李戴,没有弄清各自模型的区别与联系。
破解之道:解决此类问题,最佳途径就是将每个模型列成表格,相关公式自己亲自动手推导一遍。推导的过程中一定会存在卡点,想不明白的地方通过回归课本以及借助网络,将其理解透彻。再结合一些专题(复习时的专项题目)、母题回头看,便会了然于心。
23年之前历届高考涉及到的概率统计基本上是这种情况。
新概念、新定义问题:对于新概念新定义问题,这类问题往往高大上,大家多数是没有接触到的,可寻古也可论今,多个概念绕来绕去,不知所云。
实际上这类题往往是理解起来困难,做起来简单。将每个概念通过列表或画图,弄清其基本概念和内在联系,题目也基本上就能顺利解答出来了。因此,强烈建议多花点时间,用在题意理解上!因为大家要考130分以上,甚至145分(强基计划),就必须拿下这道题的!24年是不是会考这样的题,我们拭目以待!



