七个圈填入1-7个自然数,使每边三个数的和是10,该怎样分配这1、2、3、4、5、6、7这七个自然数呢?有没有看出来这道题目似乎看着难,但是其实是小学二年级的数学题,该怎么去解?小学二年级数学辅导小编来为咱们同学们算一下,我给出两种解答方法,你们认为哪一种自己好理解,就着重学习哪一种吧。
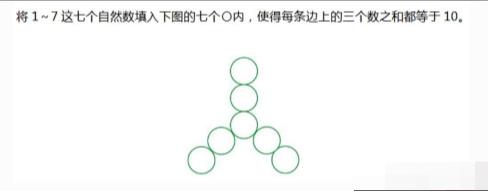
解法一:一道小学二年级数学题,怎么做?看似简单,做对的人不多?这道题看起来特别难,但是仔细想想,还是简单的。
中间那个圆填1,然后依然填上,如下计算:
2+7+1=10。
3+6+1+10。
4+5+1=10。
之前还玩过一道题,9宫格中,填上1~9,要求是横,竖的,斜的连线上的三个格子里的数字之后都等于15。
大家会吗?
老师提示大家一下,9宫格中,中间那个格子填上5。剩下的大家再自信推敲吧。
解法二:这道题看似很难,其实很简单。首先我们可以设中间那个圆圈为“位置”,把它设为x。接下来我们可以算出七个圆圈数字之和为多少,即1+2+3+4+5+6+7=28。回到刚才,列出草稿图,因为题目说了每条边上的三个数之和等于12,如果去掉x,剩下的两个圆圈之和就等于12-x。不算x,算上旁边的六个圆圈之和等于(12-x)*3,从而列出方程(12-x)*3+x=28,使用乘法分配律将方程改编为
12*3-3x+x=28
再改编为36-2x=28
求出x=4,剩下的六个圆圈随你怎么填,只要与“”在同一条线上的两个圆圈所填的数字之和是8就好了
以上虽然对七个圈填入1-7个自然数,使每边三个数的和是10的解答都使用的的方程,但是较重的结果是一样的,小学二年级数学辅导小编更喜欢第二种思想。



