甲乙两车间人数比7:4,从甲调18人则两车间人数相等,那么甲乙原来多少人?这道应用题的解题思路应该是怎么样的呢?看题目的意思,其中涉及到了比例7:4,那么这个比例关系就是解题的关键。下面小编来分享解这道问题应该使用怎样的方法,需要学生具备什么样的思路。
答案一:
解题思路:
1、甲、乙人数比是7:4,遇见此类比例题;
直接设甲7K,则乙为4K。(K是未知常数)
2、甲调走18人,剩下的人数则为:7K一I8;
3、乙调来18人,现在的人数则为:4k+18;
4、找甲乙之间的关系,由题意知调人之后两车间人数相等:
则 7K一18 = 4k + 18,解得k=l2。
则甲原来7x12=84人,乙原来4x12=48人。
答案二:
先上答案:甲车间原有84人,乙车间原有48人。这是一道比例应用题,我们可以它转化为差倍问题,关键是找到题目中隐藏的两车间人数差。
找隐藏差
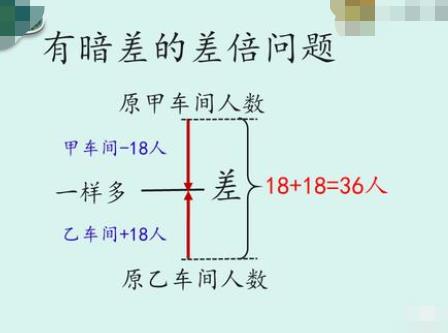
甲车间调出18人到乙车间 → 两车间人数相等,甲乙两车间人数差可不是18人哦!
还是上图会清楚理解。调整前两车间人数相差:18+18=36人。
解题步骤
把比例关系转化为份数关系,原甲为7份,乙为4份,原来两车间差36人。如下图:
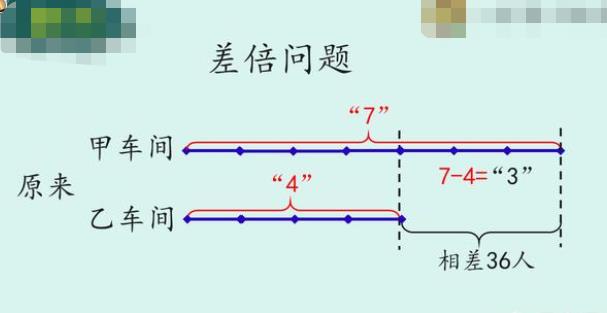
数量关系为:7-4=3份=36 。
→ 1份量:36÷3=12人。
甲为7份:12×7=84人;
乙为4份:12×4=48人。
答案为:原来甲车间有84人,乙车间有48人。
从上面两个回答中,我们能够得出甲乙别原来是84人和48人。小学数学辅导小编今天就为同学们分享到这里,如果你也是数学这块有问题的话,可以联系小编。



