求阴影部分面积的是初中几何数学的难点，更是常考的考点，我知道有很多的学生这部分的知识总是学不好，一遇到几何求阴影就眼大。类似这道问题：M是斜边的中点，n是cm和ad的交点，求阴影部分面积?便是数学几何中常常考的一类型，下面会详细解答一下这道题目，帮助同学们更好的掌握如何去求阴影部分面积。
求下图阴影部分的面积。
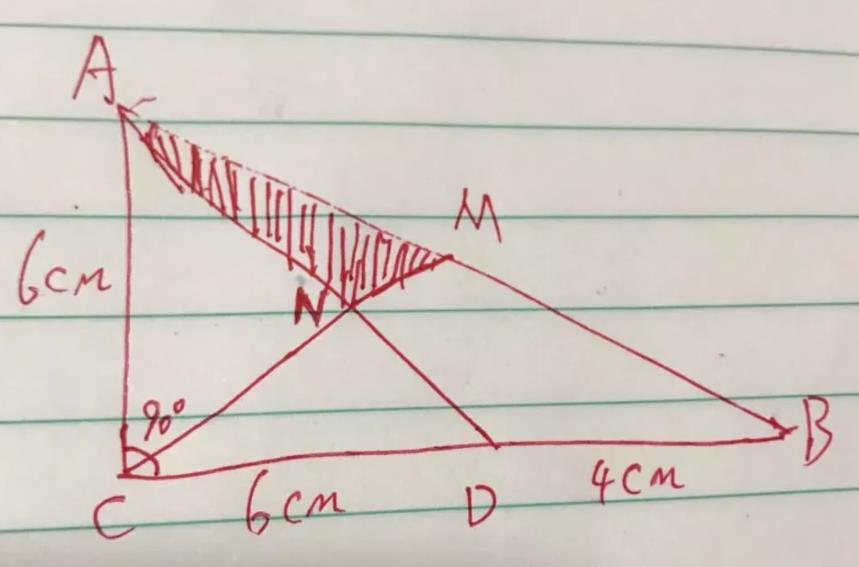
把这个图形放在直角坐标系中，则得如图所示:
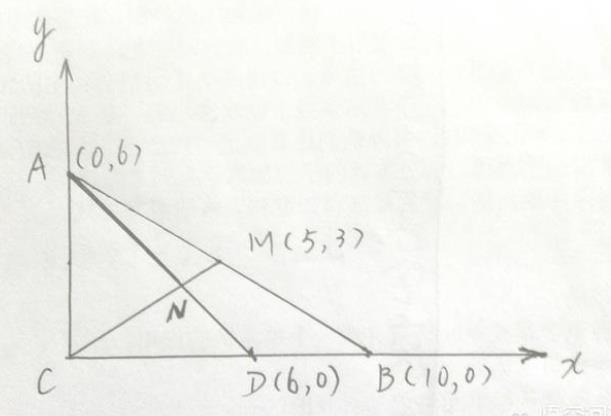
解:直线AD的方程为:y=-×+6，直线CM的方程为:5y=3x。联立方程组，
y=-x+6 ①
5y=3x ②
求得N点横轴坐标x的值为15/4，即△ANC的高。
作MH1⊥AC，MH2⊥AC，如图:
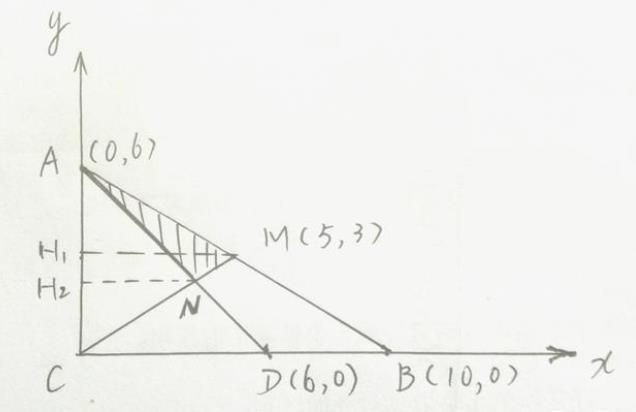
阴影部分面积:
S△AMN=S△AMC-S△ANC
=AC×MH1÷2-ACxMH2÷2
=6×5÷2-6×(15/4)÷2
=15-11.25
=3.75。
解毕。
电话咨询
在线咨询
