二次函数的较值问题怎么求?这是中考较常见的一个考点,初中时期我们学习的二次函数是是y=ax²+bx+c,c(a≠0,x∈R)的形式。咱们需要掌握这个函数的图像,初中二次函数的图像通常都是抛物线,既然是抛物线,那么肯定是有较值点的,中考出二次函数的大题,一般都会要求学生们求二次函数的较大值或者是较小值。
二次函数较值求解一般与函数的开口方向、顶点坐标、取值范围有关,下面分情况说明基本求法,以下题图均以开口向上为例,开口向下依此类推即可。
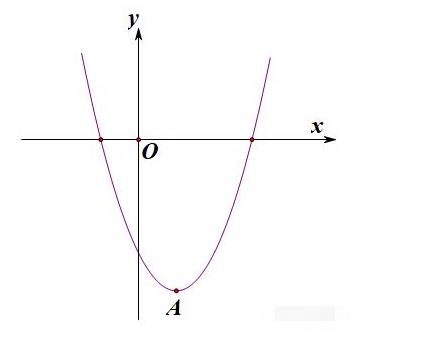
这是较简单的一种较值求法,只需要求出顶点A的坐标即可,纵坐标即为该二次函数较小值。
如果带有自变量取值范围,那么问题相对复杂一些,如上图所示,虚线即为自变量范围,注意观察,其顶点A并不在范围内,那么只能取范围的端点极值作为二次函数较值。这种情况下要特别注意取值范围中,是否包含端点,只有在包含端点的时候,才能取到较值,否则不存在。
如果自变量范围将顶点包含在内,那么类似于第一种求法。
其实求二次函数y=ax²+bx+c的较大值和较小值的方法还有很多,不同的题目选择不同的方法求会比较简单一些,其它二次函数的较值求法后面有机会再分享。



