函数问题是贯穿中小学直到未来的大学、研究生,函数问题很多,比如函数的极限性,其实是一个较难理解的问题,如果不能够说的通俗易懂,可能很多的学生是没有办法理解的。其实要小编来说函数的极限问题要说清楚,得要让孩子具备极限思想。如何将这个“极限思想”讲清楚,初高中数学辅导小编还是有一些心得体会的。
关于极限,我们一直在强调极限思想。书上的说法更加的严密,如果你要一个通俗易懂的,那么一句词就解决问题了:无限接近。就是当函数自变量x趋近于某个值的时候,我函数的因变量y也无限接近一个数。
教材上的也是这个意思。就是用ξ-Ν语言来表述:
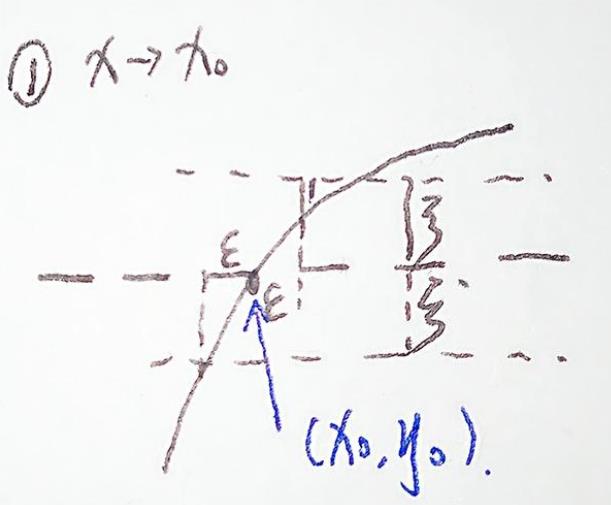
你要学会看这个图,教材是分两种情况讨论的,我们先看第一种情况当x趋近于某个具体值的时候,那么你任给一个值ξ(指的是函数上任意一点的纵坐标与y0的纵坐标之差),无论你给的有多么的小,我都能够找出一个ε,只要我x与x0的距离在这个ε之内的,我这个区间内的函数就都能满足使函数值变化不过ξ的要求。你可能会说这个图右上角有一部分满足你的要求又不在我说的区间之内,我说这是正常的,就像衣服的边角料一样,只要我区间内x的都可以满足函数值在你的区间之内就可以了。至于外面的我不用管。还有一种情况是针对x趋近于无穷的:
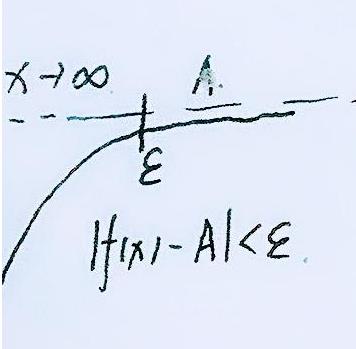
就是说当x趋近于无穷的时候,那么你任给一个数字ε当做函数与y=A的距离,这回我不变了,你去找吧,只要x大于某个X(一个具体的数字),从此以后的值都是比你给的距离小的。
函数的极限,其实就是“无限接近”,无限接近主要是两个未知数x个y之间的关系,当x无限的变化时,你要看y是如何变化的,这就是它们之间的函数关系。



