马上就要开启2019年秋季学期的期中考试了，这是一学期的中间段的小口考，重要程度仅次于期末考试。不知道各位同学们复习的怎么样了，对于定型类型的题目有没有做的训练。初中几何问题中经常会考一些几何证明类题目，这道过△ABC顶点A向B、C的外角平分线作垂线AF、AE，垂足是F、E，证明EF长等于 ABC周长之半。便是很典型的题目，你们知道怎么准确的证明结果吗?

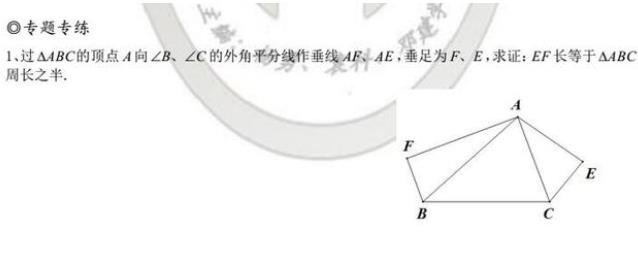
　　证明：

　　分别延长 AF 、BC、 AE 交于G 、H 两点，连接 EF 如下图所示：

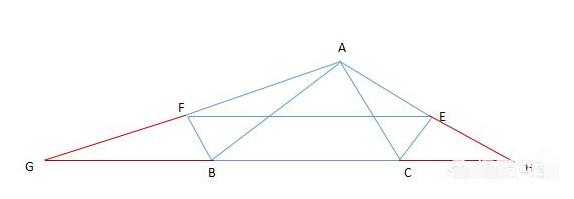
　　∵ BF⊥AF ∴ ∠BFG = ∠BFA = 90° ;

　　∵ BF 为△ABC 外角 ∠ABG 的角平分线，

　　∴ ∠GBF = ∠ABF

　　在△GBF 和 △ABF 中，

　　∠GBF = ∠ABF，BF = BF , ∠BFG = ∠BFA = 90° ;

　　∴ △GBF ≌ △ABF (ASA)

　　∴ FG = GA , BG = BA

　　∴ 点 F 为 AG 的中点

　　同理可证： 点 E 为 AH 的中点，CA = CH 。

　　∵ 在△AGH中 EF 是中位线，则有 EF 平行且等于 1/2 GH，

　　∴ EF = 1/2 GH = 1/2 (BG + BC + CH)

　　∵ BG = BA ， CA = CH

　　∴ EF = 1/2 (BA+ BC + CA)

　　即证 EF 的长等于△ABC 周长的一半。

　　以上详细的证明过程就是过△ABC顶点A向B、C的外角平分线作垂线AF、AE..证明EF长等于 ABC周长之半这道问题的解法，同学们仔细的看一下，说不这次期中考试会考到。