图3-5-1是抛物线形拱桥，当拱顶离水面2米时...水面宽度将增加多少米?省略号的条件是水面宽4米，如果水面下降1米。那么水面的宽度将会增加多少米呢?将这个条件连起来就是整道问题了，图形展示如下图。这是一个二次函数的解析问题，所以需要利用二次函数的解析式来解决这个问题。

　　一、建立平面直角坐标系：

　　以水面BC为 x 轴，拱顶到水面的距离 DO 为y 轴建立如下图所示的平面直角坐标系。

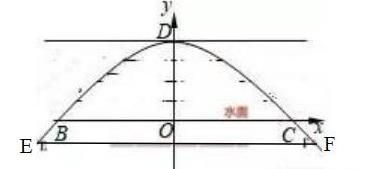
　　二、确次二次函数的解析式：

　　(3种方法：一般式，顶点式，两根式。)

　　主要结合题中信息来选取哪种!

　　因为水面的宽为4米，

　　所以点B(—2，0)，点C(2，0)。

　　又因为拱顶到水面的距离是2米，

　　所以点D(0，2)。

　　选取“两根式”：

　　设解析式为： y = a(x—x1)(x—x2)，

　　(注：a<0，x1=—2，x2=2)，

　　则有：

　　y=a(x+2)(x—2)，

　　把D(0，2)代入解析式得：

　　2 = —4a，解得：a = —0.5

　　所以二次函数解析式为：

　　y= —0.5x^2 + 2 。

　　三、解决实际问题：

　　因为水面下降1米变为EF，则来比较EF和BC(4米)的长度，也即是水面增加的宽度。

　　这是已知 y 来求 x。

　　则有：

　　—1 = —0.5x^2 + 2 ，

　　解得：x = ±√6 ，

　　所以：E(—√6，0)，F(√6，0)，

　　则EF = 2√6 ，

　　较后水面增加的宽度为：

　　EF — BC = 2√6 — 4 (米)。