新高考对于相关概念的理解提出了更高的要求!本节结合相关的案例,针对同学们普遍存在的导数理解偏差予以说明。概念理解透了,做起题来也就得心应手了。
案例一: 如下图:分段函数的单调性
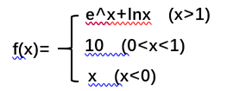
【错解】f(x)是一个分段函数x>1时,f’(x)>0;0<x<1时,f’(x)=0;x<0时,f’(x)>0,推出f’(x)≥0。所以说f(x)在整个定义域内单调递增。
【错在哪里】导数判断的是连续区间,这也是定义中给出的在区间内可导的意义!分段后则不一定连续,所以要验证端点值。高考的综合导数题也会出一些端点效应的题目(使用洛必达法则求解更为方便)
案例二:y=f(u),u减小,y增大;u=g(x),x增大,u增大;那么y=f(g(x))的单调性是?
复合函数单调性:内外函数单调性相同,复合为增,内外函数单调性相反,复合为减。
这里要说明的是,只需要分别判断内层和外层函数的单调性是否相同,而具体的是内层增还是外层减,亦或是内层减外层增,则复合起来的函数都是递减函数。
【特别注意外层函数的定义域是内层函数的值域,不要随意扩大外层函数的定义域】
高考题目会怎样出?
案例三:已知f(x)=x^3+ax+b对任意的x1,x2,在(0,√3/3),且x1!=x2,都有|f(x1)-f(x2)|<|x1-x2|,求a。
【解析一】本题是一个典型的存在性问题,历年高考涉及的较多。解题的关键(题眼)就是|f(x1)-f(x2)|<|x1-x2|。容易看出的就是|f(x1)-f(x2)|/|x1-x2|=|f’(x)|<1。这里利用|f’(x)|的范围,并结合x的范围,可以解出来。难点就是怎么理解“任意的x1,x2”。
【解析二】本题换种思路来解决。构造函数。设x1>x2,则|f(x1)-f(x2)|<|x1-x2|,脱去绝对值可以转化为x2-x1<f(x1)-f(x2)<x1-x2,进一步变形为:f(x2)+x2<f(x1)+x1①式 和 f(x1)-x1<f(x2)-x2 ②式。构造函数g(x)=f(x)+x,在(0,√3/3)单调递增;构造函数m(x)=f(x)-x,在(0,√3/3)单调递减。g’(x)≥0且m’(x)≤0,从而解得a的范围。
这里要特别提醒大家注意的是,变量的归一思想,想一想为什么要将含x1和x2的分别移动到不等式的两边。这也是平常我们做题时常用的思想。
【解析三】数形结合,充分利用割线与切线。这里需要提一下“拉个朗日中值定理”:若函数f(x)在(a,b)上可导,[a,b]上连续,则必有ξ €(a,b),使得f’(ξ)=[f(b)-f(a)]/(b-a)。那么上题我们先设x1<x2,转化为在(0,√3/3)存在一点设为x0,使得f’(x0)=[f(x2)-f(x1)]/[x2-x1]成立。而x0的范围就是x的范围,要是的x范围内所有点满足,显然是一个恒成立问题。即|f’(x0)|<1,满足。结合看一下f’(x)的单调性,和f’(x)的范围,找到极值点对应的x值带入f’(x),即可求出a值。
这里要特别注意的是,很多同学直接讲x的范围的端点(0,√3/3)带入了f’(x)中,获得结果一般来讲是不正确的,高考题一般不会让f‘(x)只具有简单的单调性,至少是复杂一点的二次函数。
如果再学习数学中遇到困难,报高三数学辅导班也是很好地选择,它是一种专门针对高三学生的数学学科辅导服务,由经验丰富的教师团队组成。参加高三数学辅导班可以在学术上获得更好的学习效果,因为这种辅导班通常侧重于高考数学考试的内容和题型,有针对性地进行教学。在辅导班中,学生能够系统地复习基础知识,解决难题,提高解题能力。
同时,辅导班的教师会根据学生的学习状况进行辅导,及时发现和纠正学习中的问题,帮助学生更好地理解数学概念,提高应试水平。通过参加高三数学辅导班,学生能够更有针对性地备战高考数学科目,提高考试成绩。



