新高考的题目会以独特的形式呈现,而难题常常会被混淆或隐藏。对于多数考生来说,题目一旦被遮掩,就变得陌生了。在这种情况下,仔细审题并理清各条件之间的实际含义至关重要,这是解题的关键。以下以概率统计部分为例进行阐述。

概率统计部分的压轴题,关键在于准确理解题意。务必反复阅读,深入思考题目的含义,并将其转化为数学语言,以便找出与核心知识点相对应的模型。
要达到这种能力,需要对概率统计部分相关概念无歧义的深入理解,弄清各模型【古典概率问题?几何分布与超几何分布与二项分布?数学期望与分布律?正态分布?】等等适用的条件。在开始本节之前,先来弄清以下几个概念。
期望值并不一定等同于常识中的“期望”——“期望值”也许与每一个结果都不相等。期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里。大数定律表明,随着重复次数接近无穷大,数值的算术平均值几乎肯定地收敛于期望值。
如果随机变量只取得有限个值或无穷能按一定次序一一列出,其值域为一个或若干个有限或无限区间,这样的随机变量称为离散型随机变量。
数学期望与分布律之间的关系:
![]()
接下来用两道经典例题,一步步详细解析来说明在高考中遇到概率与统计问题,如何正确无误的解答出来。

在看答案之前,大家先行解读一下题目内容,并转化成自己的话,叙述出来,看看有没有歧义。这一点非常之关键!一定要做。此外,在遇到没有思路的题目时,关注思考的参考答案解题的顺序也是至关重要的。
【解析】①理清题设各条件的关系。这类题画个流程图是关键,理清关系了,基本上就成功了80%。
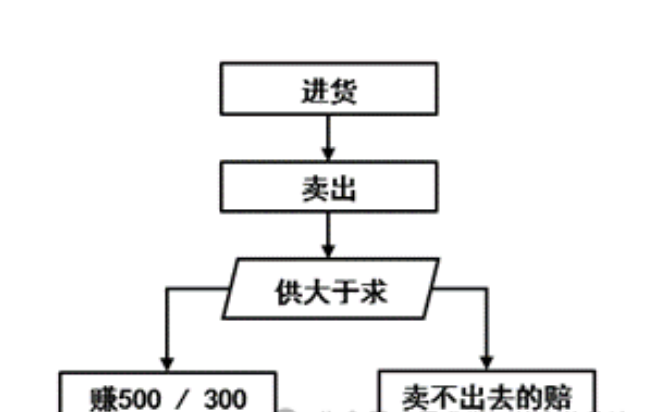
②深入题目分析找模型。本题题设给出了3个名词,需求量【离散型随机变量】、进货量【离散型随机变量】、利润。分别设其为X、m、Y。待求量是利润最大的期望。其模型是典型的数学统计里的期望问题。
③题设数学语言的转化。我们想一下,如何计算利润?一般的计算方法是利润=销售额-成本。这里单价没给出,但是给出了某种情况下,卖出一单的利润分别为500、300;以及某种情况下会亏损100。我们来讨论一下这里的“不同情况”与“某种情况”。
④解题关键找状态。本题中的不同情况有两种,供不应求是第一种,在此条件下的利润为自己进货卖出的和从其他店调货卖出的,即:Y1=500m+300(X-m);第二种情况是供大于求,利润为卖出的减去没有卖出的(这里是难点),即Y2=500X-100(m-X)。对应题干是削价处理,每件赔100元。(因100元是在成本基础上赔的,故也不需要考虑成本)。
Y1=500m+300(X-m) ;Y2=500X-100(m-X)这两个式子看着是不是很简单。但是逻辑性确实很强的,仔细体会。达到一通百通的目的。
⑤带入期望的相关公式。找到了Y关于X的函数带入期望的数学公式。进而利用函数求最值的思想,求解即可。(答案是每周最大进货量23.3,最大利润的期望是9333.3)



